
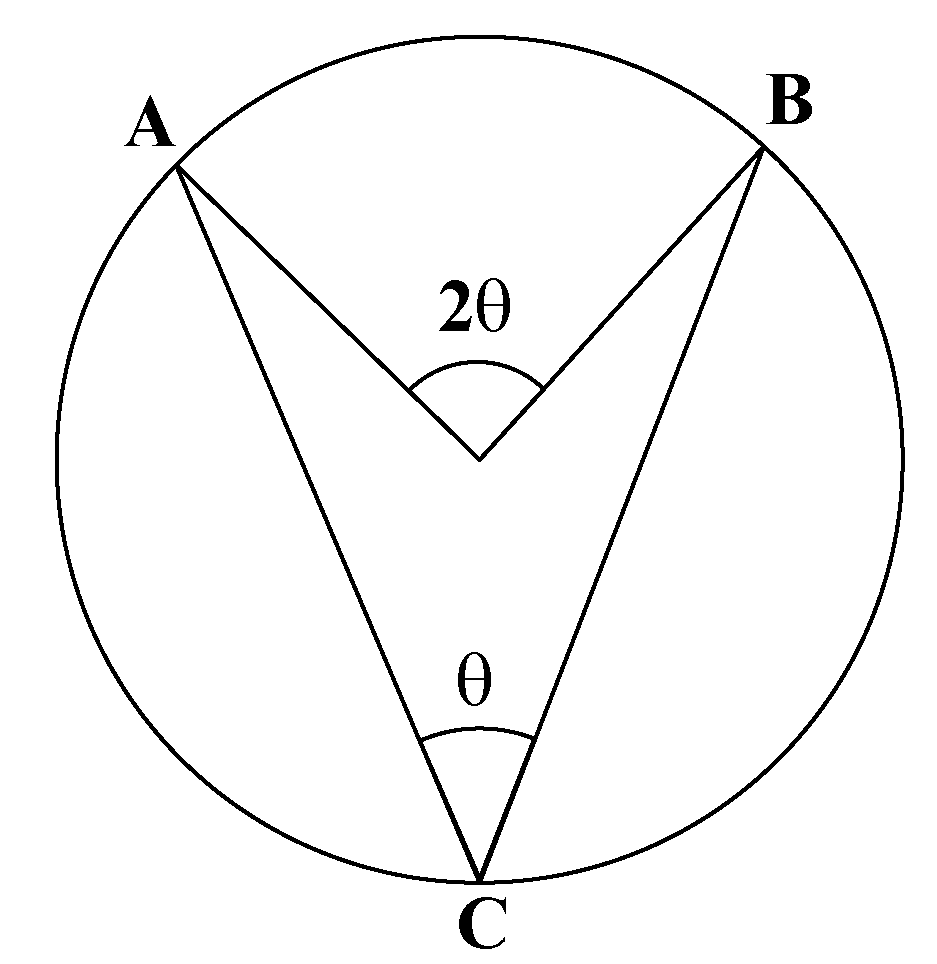
Varsity Tutors does not have affiliation with universities mentioned on its website. Media outlet trademarks are owned by the respective media outlets and are not affiliated with Varsity Tutors.Īward-Winning claim based on CBS Local and Houston Press awards. So, the central angle subtended by the chord is 127.2 degrees.Names of standardized tests are owned by the trademark holders and are not affiliated with Varsity Tutors LLC.Ĥ.9/5.0 Satisfaction Rating based upon cumulative historical session ratings through 12/31/20. Now calculate the angle subtended by the chord. Therefore, the length of the chord PQ is 36 cm.Ĭalculate the length of the chord and the central angle of the chord in the circle shown below. Thus, the perpendicular distance is 6 yards.Ĭalculate the length of the chord PQ in the circle shown below.īy the formula, length of chord = 2r sine (C/2) Given that radius of the circle shown below is 10 yards and the length of PQ is 16 yards. Therefore, the radius of the circle is 25 inches.
Length can never be a negative number, so we pick positive 25 only. Suppose the perpendicular distance from the center to the chord is 15 inches. The length of a chord of a circle is 40 inches. Calculate the chord’s length if the circle’s diameter is 34 m.ĭiameter, D = 34 m. The perpendicular distance from the center of a circle to the chord is 8 m. Given radius, r = 14 cm and perpendicular distance, d = 8 cm,īy the formula, Length of chord = 2√(r 2−d 2) The radius of a circle is 14 cm, and the perpendicular distance from the chord to the center is 8 cm. Let’s work out a few examples involving the chord of a circle. If the radius and central angle of a chord are known, then the length of a chord is given by,Ĭ = the angle subtended at the center by the chordĭ = the perpendicular distance from the center of a circle to the chord. The length of a chord, given the radius and central angle.In the above illustration, the length of chord PQ = 2√ (r 2 – d 2) Where r = the radius of a circle and d = the perpendicular distance from the center of a circle to the chord. If the length of the radius and distance between the center and chord is known, then the formula to find the length of the chord is given by, The length of a chord, given the radius and distance to the center of a circle.Each formula is used depending on the information provided. There are two formulas to find the length of a chord.
For example, chord AB is equal to chord CD if PQ = QR. Two chords are equal in length if they are equidistant from the center of a circle.Two radii joining the ends of a chord to the center of a circle form an isosceles triangle.The diameter is the longest chord of a circle, whereby the perpendicular distance from the center of the circle to the chord is zero.The length of a chord increases as the perpendicular distance from the center of the circle to the chord decreases and vice versa.The radius of a circle is the perpendicular bisector of a chord.In the circle below, AB, CD, and EF are the chords of the circle. The diameter of a circle is considered to be the longest chord because it joins to points on the circumference of a circle.
#Central angle geometry definition how to#


 0 kommentar(er)
0 kommentar(er)
